1. 테일러 방법
1) 테일러 방법이란?
수치 해석적인 방법으로 미분방정식의 근사해를 찾는 방법

2) K차 테일러 방법
주어진 미분방정식을 만족하는 해의 k+1계 도함수 y^(k+1)이 [a,b]에서 연속이라고 하면 테일러 전개에 의하여 적당한 ξ∈[t,t+h]가 존재하여 다음 식이 성립
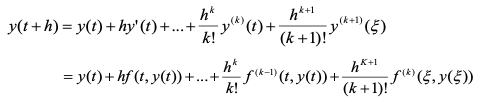
h가 0보다 작으면 hK+1은 매우 작게 되므로 t=t(n+1) (=tn+h)에서 다음 식이 성립

K차 테일러 방법이란
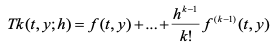
라 하면 다음 반복식에 의하여 해를 구하는 방법

1차 테일러 방법
- T1(t,y;h)=f(t,y)이므로 1차 테일러 방법은 오일러 방법이 됨.
- y는 t에 관한 함수이므로 함수 f(t, y)역시 t에 관한 함수
- k가 1보다 클 경우 고계도 함수를 사용해야 하는 어려움이 존재

3) 예제풀이 1
2차 테일러 방법을 이용하여 다음 방정식의 해의 근사값을 구하여라. 단, h=0.2

풀이

4) 예제풀이 2
2차 테일러 방법을 이용하여 다음 방정식의 해의 근사값을 구하여라. 단, h=0.2

풀이
다음표와그래프는y0,...,y10의결과이며,이방정식의해는 y=e^(5x)^2

5) 테일러 방법 알고리즘
알고리즘의 목적
- 미분방정식의 수치해를 구하기 위한 알고리즘
알고리즘의 변수

다음 방정식의 근사값을 구하는 알고리즘을 완성해보자(단, h=0.2).

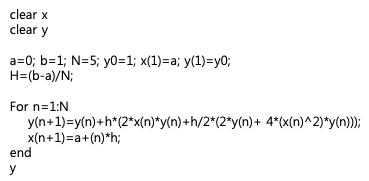
2. 룽게-쿠타 방법
1) 룽게-쿠타 방법
목적
- 초기치미분방정식 y’(t)=f(t,y),a≤t≤b,y(a)=y0의 수치적인 해를 구하는 것으로 오일러 방법이나 테일러 방법에 비해 비교적 오차가 적음
Heun의 방법

개량된 오일러의 방법

4차 룽게-쿠타 방법

- 테일러 방법은 차수가 높으면 고계편도함수를 구해야 하는 단점
- 룽게-쿠타 방법은 반복식에서 증분함수를 적당하게 선택하여 고계편도함수를 사용하지 않고
- 근사값을 구할 수 있음
- 2차 룽게-쿠타 방법은 반복식에 a, b, α, β 를 구하여 사용하는 방법

2) 증분함수와 Heun의 방법
증분함수
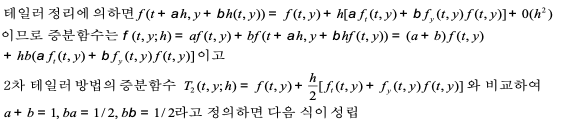

Heun의 방법
Heun의 방법 : 위의 식을 만족하는 다양한 a, b, α, β에서 a=b=1/2, α=β=1로 택한 반복식

개량된 오일러 방법 : Heun의 방법에서 a=0, b=1로 택한 반복식

3) 예제풀이
(1)
Heun의 방법과 개량된 오일러 방법을 이용하여 다음 방정식의 해의 근사값을 구하여라. 단, h=0.1
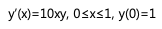

(2)
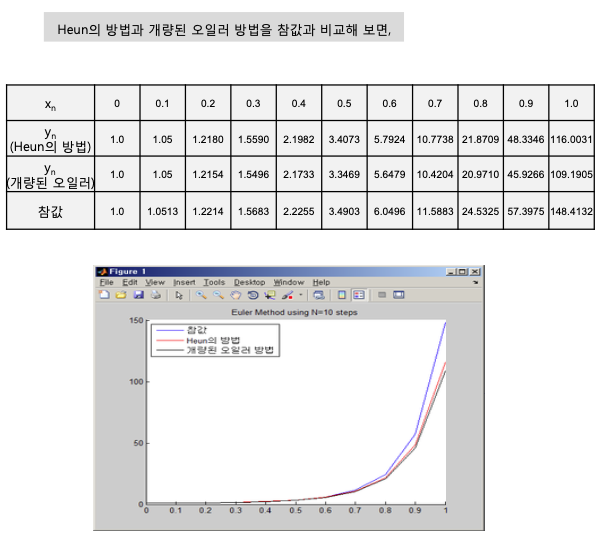
Heun의 방법과 개량된 오일러 방법을 이용하여 다음 방정식의 해의 근사값을 구하여라. 단, h=0.1


4) Heun의 방법 알고리즘
알고리즘의 목적
- 미분방정식의 수치해를 구하기 위한 알고리즘
알고리즘의 변수


5) 개량된 오일러의 방법 알고리즘
알고리즘의 목적
- 미분방정식의 수치해를 구하기 위한 알고리즘
알고리즘의 변수
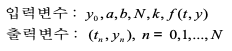
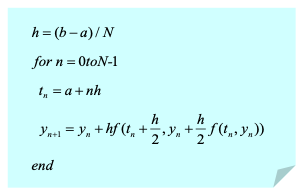
6) 예제풀이
다음 방정식의 근사값을 구하는 알고리즘을 완성해보자(단, h=0.1).


7) 4차 룽게-쿠타 방법 반복식
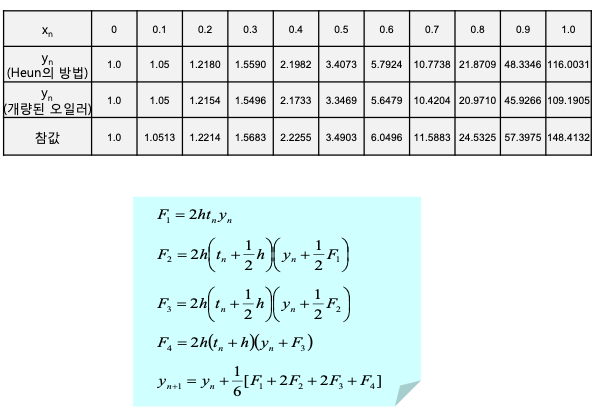
- 표의 값들을 비교할 때 Heun의 방법이 가장 참값에 근사
- 그러나 그 외의 방법도 모두 참값에 근사
- 더 큰 차수의 룽게-쿠타 방법도 같은 방법으로 유도 가능
- 차수가 높을 수록 오차는 작아지나 계산량은 그만큼 많아짐.
- 일반적으로 많이 사용되는 4차 룽게-쿠타 방법의 반복식
8) 적용하기
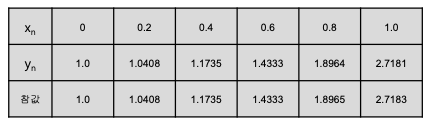
4차 룽게-쿠타 방법을 이용하여 다음 방정식의 해의 근사값을 구하여라. 단, h=0.2
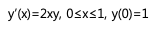
풀이

이므로

와 같은 방법으로 다음과 같은 표를 얻는다.
9) 4차 룽게-쿠타 방법 알고리즘
알고리즘의 목적
- 미분방정식의 수치해를 구하기 위한 알고리즘
알고리즘


10) 적용하기
다음 방정식의 근사값을 구하는 4차 룽게-쿠타 방법의 알고리즘을 작성해보자. (단, h=0.2)


'수학 > 수치해석' 카테고리의 다른 글
| 16차시 - 최소자승법 (0) | 2020.04.02 |
|---|---|
| 14차시 - 미분방정식과 해 1 (2) (0) | 2020.03.31 |
| 14차시 - 미분방정식과 해 1 (1) (0) | 2020.03.31 |
| 13차시 - 수치적분(2) (0) | 2020.03.30 |
| 13차시 - 수치적분(1) (0) | 2020.03.30 |



