3. 복합수치적분
1) 수치적분 복합공식
복합수치적분
- 일반적으로 Newton-Cotes 공식은 적분구간이 큰 경우에 적당하지 않음
- 큰 구간에서 고차의 공식을 사용
- 고차 공식의 계수를 구하기가 어려움
- Newton-Cotes공식은 같은 간격의 점들을 이용한 보간다항식을 사용
- 고차 다항식은 큰 구간에서 진동하는 성질 때문에 진동하는 성질 때문에 정확도가 낮음
- 구간 [a,b]를 균등하게 n개의 소구간으로 분활하여 각각의 소수간에서 정밀도가 낮은 수치적분법을 시행해여 그 결과값을 모두 합하는 방법을 복합수치적분이라 함
2) Simpson 복합공식

- 구간을 세분화하여 Simpson공식을 사용하여 오차를 줄 일 수 있음
- 구간 [a, b]를 2m개의 작은 구간으로 나눈다고 가정
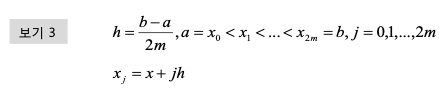
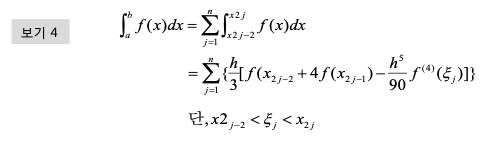
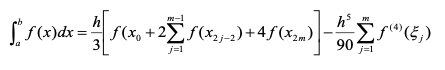
3) Simpson 복합공식 알고리즘

4) MATLAB을 이용한 수치적분 Simpson 복합공식
다음은 심프슨 공식을 이용하여 적분값 f (x) = x2일때, ∫(1,3) f (x)dx 을 매트랩으로 구하여라.

5) 사다리꼴 복합공식
- F∈C^2[a,b]라 할 때, h=(b-a)/m이고, 각 j=0, 1, ..., m에 대하여 xj=a+jh 일 때, 사다리꼴 복합공식은 보기 1과 같음.

6) 사다리꼴 복합공식을 이용한 복합수치 적분 예

7) 사다리꼴 복합공식 알고리즘

8) MATLAB을 이용한 사다리꼴 복합공식
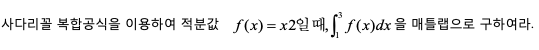

'수학 > 수치해석' 카테고리의 다른 글
| 14차시 - 미분방정식과 해 1 (2) (0) | 2020.03.31 |
|---|---|
| 14차시 - 미분방정식과 해 1 (1) (0) | 2020.03.31 |
| 13차시 - 수치적분(1) (0) | 2020.03.30 |
| 12차시 - 수치미분 (0) | 2020.03.24 |
| 11차시 - 반복법과 역행렬 (2) (0) | 2020.03.17 |



