3. 가우스 소거법
1) 가우스 소거법이란?
- n개의 방정식과 n개의 미지수로 이루어진 일반적인 선형 연립방정식 Ax = b의 해를 구하는 방법
- 해를 구할 수 있도록 문제의 방정식과 동치인 상삼각연립방정식 Ux = Y를 구성
-> 동치란 해집합이 동일한 두 개의 n x n 선형 연립방정식을 뜻함. - 선형 대수학의 정의로부터 주어진 선형 연립방정식을 특별한 방법으로 변환하면 해집합은 변하지 않음.
- 방정식 개수가 수십개인 작은 크기의 연립방정식에서 실근에 매우 근접한 해를 구할 수 있음.
- 선형연립방정식에 다음 연산을 적용하면 동치인 선형 연립방정식을 구할 수 있음.
기본행연산
- 교환(interchange) : 두 방정식의 순서를 바꾼다.
- 크기조정(scaling) : 방정식에 0이 아닌 상수를 곱한다.
- 대체(replacement) : 방정식에 다른 방정식의 상수 배를 더하거나, 빼는 방법으로 기존의 방정식을 대체한다.
2) 가우스 소거법 연산과정
- 가우스 소거법을 이용하여 선형연립방정식의 해를 구하는 방법은 크게 2단계
-> 가우스 소거법을 이용하여 선형연립방정식의 해를 구하기 위해서 첨가행렬을 사용
첨가행렬
- 선형연립방정식을 풀기 위해 Ax=B의 모든 계수를 차원이 n x (n+1)인 배열에 저장
- B의 계수들은 그 배열의 n+1번째 열에 저장
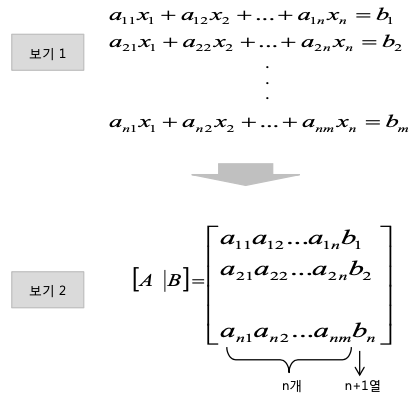
상삼각 행렬화
- a(11)이 0이 아니라고 가정
-> 만일 0일 경우 a(k1)이 0이 아닌 방정식과 첫 번째 행을 바꿈 - 앞에서 학습한 기본행연산 중에서 대체를 이용하여 a(21),...., a(n1)을 0으로 만듦
-> 첨가 행렬의 첫 번째 행에 a(i1)/a(11)을 곱하여 그 행렬의 i번째 행에서 빼는 과정을 i=2에서 n까지 모두 실행하면 아래와 같은 행렬 (A | b)(2)로 변환
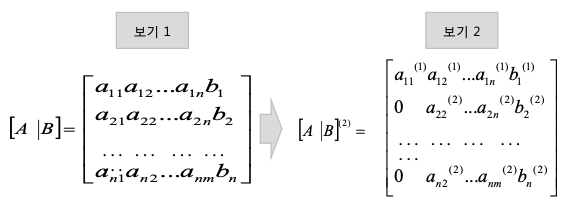
- 위와 같은 과정을 반복하여 대각선 아래 항이 모두 0이 될 때 까지 계속 수행하여 다음과 같은 상삼각행렬을 구함

역 대입 단계
- 상삼각행렬화한 첨가행렬을 다시 연립방정식의 형태로 표현

- 아래 식으로부터 xn을 구할 수 있음.
- xn를 n-1번째 연립방정식에 대입하여 x(n-1) 의 값을 구함.
- 위 과정을 반복하여 x(n-1) 부터 x1 까지 구함.
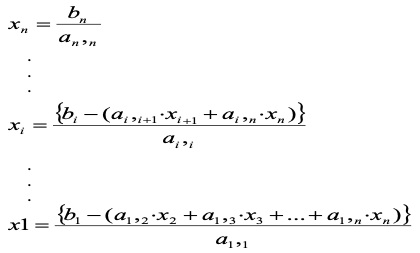
3) 가우스 소거법 연산 예
- 행렬 A, b가 다음과 같이 주어진 경우, 가우스 소거법을 이용하여 해를 구함
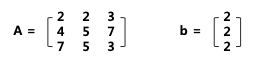
- 다음과 같이 첨가핼렬을 만듦

- 기본행 연산을 통해 첨가행렬을 상삼각행렬로 만듦
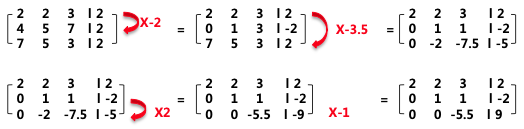
- 역대입을 통해 해를 구함

4) MATLAB을 이용한 가우스 소거법
clc; clear all; close all;
A = [2,2,3;4,5,7;7,5,3]
B = [2;2;2]
[n,n2] = size(A);
[k2,k] = size(B);
z = zeros(n,k);
for(i=2:n)
m =- A(i:n,i-1)/A(i-1,i-1);
A(i:n,:) = A(i:n,:)+m*A(i-1,:);
B(i:n,:) = B(i:n,:)+m*B(i-1,:);
end
x(n,:) = B(n,:)/A(n,n);
for(k=n-1:-1:1)
x(k,:) = (B(k,:)- A(k,k+1:n)*x(k+1:n,:))/A(k,k);
end
x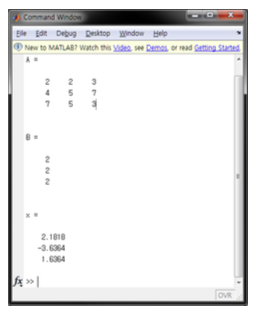
'수학 > 수치해석' 카테고리의 다른 글
| 11차시 - 반복법과 역행렬 (1) (0) | 2020.03.17 |
|---|---|
| 10차시 - 선형연립방정식과 해 (3) (0) | 2020.03.14 |
| 10차시 - 선형연립방정식과 해 (1) (0) | 2020.03.13 |
| 9차시 - 방정식의 해법 3 (2) (0) | 2020.03.12 |
| 9차시 - 방정식의 해법 3 (1) (0) | 2020.03.11 |



