1. 분할차분법
1) 분할차분법
서로 다른 (n+1)개의 점 x0, x1, x2, ⋅⋅⋅, xn에 대해서, 함수 f(x)와 함수 값이 같은 n차 이하의 다항식 Pn(x)가 다음과 같이 주어졌을 때
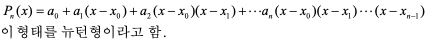
그러면 각 x값에 따라서 다음 관계가 만족하고, 이에 따라 상수항 a0 ,a1,⋅⋅⋅을 순서대로 구할 수 있음.
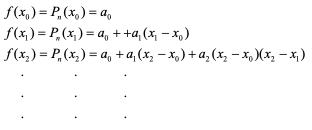
중복된 계산식(예:x1 − x0 )을 줄이기 위해, 분할 차분기호를 사용
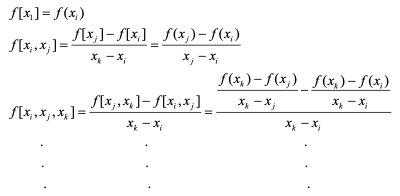
이를 일반화 시켜서 다음과 같이 표현 가능
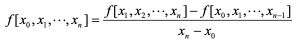
이 공식을 n차 분할차분공식이라고 함.
- 앞에서 얻은 n차 분할차분공식을 이용하여 분할차분표라는 표 제작 가능
- 이 표를 사용하면 뉴턴 공식에 있는 모든 분할차분을 간단한 방법으로 얻을 수 있음.
-
뉴턴 공식을 사용하여 보간다항식 pn(x)를 구할 때는 분할차분표의 각 열에서 처음 항들이 그 다항식의 계수가 됨.
- 다음과 같은 표를 분할차분표라고 한다.

2. 보간다항식의 오차
1) 보간다항식의 오차
f(x)가 구간 [a,b]에서 정의된 함수이고, x0,x1,⋅⋅⋅,xn을 구간 안에 있는 n+1개의 서로 다른 점이라 할 때, 차수가 n보다 크지 않은 다항식Pn(x)를 n 점 x0, x1, ⋅⋅⋅, xn에서 f(x)의 보간다항식이라 하면 이 때, 생기는 오차 en(x)는 다음과 같이 표현 가능
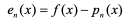
x를 주어진 점 x0, x1, ⋅⋅⋅, xn이 아닌 임의의 점이라 하자. 만일 차수가 n+1보다 크지 않은 다항식 p(n+1)(x)를 점 x0 , x1 ,⋅⋅⋅xn , x에서
f(x)의 보간다항식이라 하면 다음이 성립
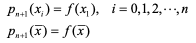
이 식은 뉴턴공식에 의해 다음과 같이 표현 가능
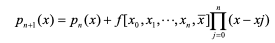
또, f(x)는 다음과 같음.

앞에서 나온 2개의 식을 통해 x ≠ x0, x1, ⋅⋅⋅, xn에 대해 다음과 같은 식을 얻음.

위의식은 f(x)을 알아야 en(x)를 구할 수 있지만, 다음 정리는 f(x)값을 모르더라도 en(x)를 구할 수 있음.
함수 f(x)가 구간 [a,b]에서 정의된 함수이고, (a,b)에서 k차 미분가능하다고 할 때, 만일 x0 , x1 , ⋅⋅⋅, xk가 [a, b]안에 있는 (k+1)개의 서로 다른 점이면,

앞에서 사용한 식과 정리를 통해 다음과 같은 정리를 얻을 수 있음.
함수 f (x)가 폐구간 [a,b]에서 정의된 함수이고 개구간 [a,b] 에서 (n+1)차 미분가능하다고 하자. 만일 pn (x)가 차수가 n보다 크지 않고 [a,b]안에 있는 (n+1)개의 점 x0 , x1 , ⋅⋅⋅, xn에서 f ( x)의 보간 다항식이라고 하면 [a,b]안의 임의의 점 x에 대해서

를 만족하는 점 ε ∈ (a,b)가 존재한다.
위 정리에서 ε는 x에 따라 결정되고 공식을 사용하려면 ε와 f (x)의 (n +1)차 도함수 f^(n+1)(x)를 알아야 함.
ε는 구간 (a,b) 안에 있는 어떤 점이라는 사실만 알고 실제로는 정확한 ε를 알 수 없고, f^(n+1) (x)도 모르는 경우가 많음.
그러나 구간 [a,b]에서 |f^(n+1) (x)| 의 상계(upper bound)를 알면 이 공식을 이용해 보간다항식의 오차의 한계를 구할 수 있음.
'수학 > 수치해석' 카테고리의 다른 글
| 7차시 - 방정식의 해법 1 (1) (0) | 2020.03.07 |
|---|---|
| 6차시 - 분할차분표와 보간법(2) (0) | 2020.03.06 |
| 5차시 - 보간다항식(2) (0) | 2020.03.05 |
| 5차시 - 보간다항식(1) (0) | 2020.03.05 |
| 4차시 - 오차해석(2) (0) | 2020.03.04 |



