1. 빈도로 수집된 자료의 분석을 위한 카이제곱 검정
1-1. 변수간의 독립성 검정
1. 가설설정
귀무가설 H0 : 두 변수는 독립이다.
대립가설 Ha : 두 변수는 독립이 아니다.
2. 검정통계량의 설정
카이제곱 분석을 위한 검정통계량은 기대빈도와 실제 관측빈도와의 차이를 제곱한 값을 기대 빈도를 기준으로 계산한 것. 다음의 식과 같이 도출. 두 변수가 독립이 아닐 경우 관 측빈도와 기대빈도는 큰 차이를 보이게 됨. 따라서 카이제곱 검정은 우측검정을 실시함.

1-2. 독립성 검정을 위한 예시
1. 가설 설정
가구소득과 냉장고 크기의 관계가 독립적인가를 파악하고자 함.
- 귀무가설 : 가구소득과 냉장고 크기는 독립이다. (무관하다)
- 대립가설 : 가구소득과 냉장고 크기는 독립이 아니다. (무관하지않다)

* 기대빈도는 가구 소득과 냉장고 크기가 독립이라는 가정하에 계산됨. 예를 들어 가구 소득이 ‘저’인 경우는 40가구이며 냉장고 크기가 소형인 경우는 전체 300명중 70명이므로 독립이라고 생각할 때 이론적으로는 40*70/300=9.33가구가 되어야 함.
2. 검정통계량의 계산 및 해석
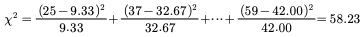
유의수준 5%에서 우측검정의 임계치는 9.49. 검정통계량은 58.23으로 임계치보다 크므로 유의수준 5%에서 가설을 기각함. 즉, 가구 소득과 세탁기 크기는 독립적이지 않음.
1-3. 집단간 응답 비중 차이 검정

1. 중요한 차이의 관찰과 귀무가설의 설정
ㄱ. 귀무가설은 집단 간 차이가 동일하다고 가정하는 것이므로 "연령별로 차이가 발생하지 않는다" 로 수립
ㄴ. 관찰된 수치를 실제 연령별 사용자 수로, 기대치를 평균값 42로 하여 카이제곱 통계량 계산

2. 적절한 통계량의 계산 및 계산된 카이제곱 통계량과 임계치의 비교
ㄱ. 계산된 카이제곱 통계량은 3.52로 도출
ㄴ. 5개 연령 집단이 있으므로 자유도는 ʻk-1=5-1=4ʼ.
ㄷ. 집단 간 차이 여부를 검정하기 위해 자유도 4일 때 유의수준 5%의 우측검정 임계치는 9.49.
ㄹ. 계산된 카이제곱 통계량은 3.52이며 우측검정의 임계치보다 작음.
ㅁ. 유의수준 5%에서는 "연령별로 제품의 소비에 차이가 발생하지 않는다"는 귀무가설을 기각할 수 없기 때문에 판매량에 연령별 차이가 있다고 볼 수 없음.
2. 분산분석
2-1. 분산분석(analysis of variance : ANOVA)의 정의
1. 분산분석이란?
분산분석은 두 개 이상의 모집단에 대한 모평균의 차이를 비교할 때 사용하는 통계적 기법. 만약 모집단이 두 개일 때라면 분산분석을 하지 않아도 상황에 따라 정규분포나 t분포를 이용하여 모평균의 차이를 분석할 수 있음.
그러나 비교 대상이 되는 모집단이 세 개 이상이 되는 경우에는 두 모집단을 각각 비교하는 것이 아니라(이 경우 세 번의 서로 다른 Z검정이나 t검정을 사용하게 됨) 한 번에 세 개의 모집단을 비교할 필요가 있음. 이러한 분석을 수행하는 것이 분산분석.
2. 분산분석의 유형
분산분석은 모집단을 구분하는 기준 혹은 요인의 수에 따라 일원분류분산분석, 이원분류분산분석, 삼원분류분산분석 등으로 구분. 대부분의 분산분석은 요인의 수가 하나인 일원분류분산분석과 요인의 수가 두 개인 이원분류분산분석을 실시함.
2-2. 일원분류분산분석
1. 가설 설정

2. 결과의 해석
F검정을 수행하며 집단내 변동 대비 집단간 변동의 차이가 크면 모평균에 차이가 발생하는 것으로 해석
2-3. 이원분류분산분석
1. 반복이 없는 이원분류분산분석
자료를 구분하는 기준이 두 개에 대하여 각각 하나의 표본을 조사하고 이에 대해 각각의 요인에 따른 급간변동이 발생하는지를 파악

2. 반복이 있는 이원분류분산분석
자료를 구분하는 기준이 두 개에 대하여 다수의 표본을 조사
- 주효과 : 각각의 요인에 따른 급간변동이 발생하는지를 파악
- 교호효과 : 두 요인이 동시에 작용할 때 급간변동이 발생하는지를 파악

3. 기타 다양한 통계분석
3-1. 판별분석
하나 이상의 독립변수를 사용하여 종속변수의 차이를 설명하는 방법. 종속변수로 설정된 범주의 어느 하나에 자료가 속할 수 있도록 판별하기 위한 식을 도출하는 것이 목적.
예) 고객의 집단을 구매량, 방문빈도, 1회 최대 구매금액, 만족정도라는 독립변수의 식으로 설정하면 새로운 고객에 대해서도 판별이 가능하게 됨

<예시>
구매량 : 40, 방문빈도 : 3, 1회 최대 구매 금액 : 7, 만족정도 : 80이라고 할 때
집단 1 : 0.233*40 + 2.581*3 + 0.848*7 + 0.623*80 - 33.277 = 39.562
집단 2 : 0.288*40 + 1.803*3 + 1.804*7 + 0.751*80 - 44.462 = 40.135
→ 집단 2로 분류 (추후 분류함수에 의해 정확히 분류된 대상의 비율(Hit Ratio)를 계산하여 판별력 평가)
3-2. 요인분석
주로 활용되는 경우는 제품이나 서비스의 주요 특성이 되는 요인을 발견하기 위한 경우. 여러 변수가 있을 때 유사한 특성을 갖는 변수들을 하나의 요인으로 설정하여 주요 요인이 무엇인가를 파악할 수 있음. 요인적재량이 높은 변수를 하나의 요인으로 묶어서 설명하는 것.
<예시>

3-3. 군집분석
조사 대상자 또는 일련의 자료들을 중요한 특성별로 집단화하기 위한 분석방법. 마케팅 영역 등의 시장 세분화에서 가장 많이 활용. 특정시장 내의 세분시장을 발견하기 위해 특정 군집 내에 포함되는 응답자들이 상호 간에는 유사하지만 다른 군집에 포함되는 응답자들과는 차이가 나는 방식으로 여러 개의 군집 또는 집단을 발견하는 방법을 군집분석이라고 할 수 있음. 5점 척도와 같이 등간척도로 응답한 자료에 적용하는 것이 일반적. 예를 들면 소비자를 몇 가지 라이프 스타일을 갖는 군집으로 표현하고자 할 때 라이프 스타일과 관련된 자료를 5점 척도 등으로 수집하여 군집의 기준이 되게 하는 것.
- 비계층적 군집화 : 사전에 군집의 수를 정한다.
- 계층적 군집화 : 사전에 군집의 수를 정하지 않고 군집화하는 규칙만 정한다.
<예시>
사전에 군집의 수를 정하는 k-means 방법 : 사전에 3개로 군집 설정
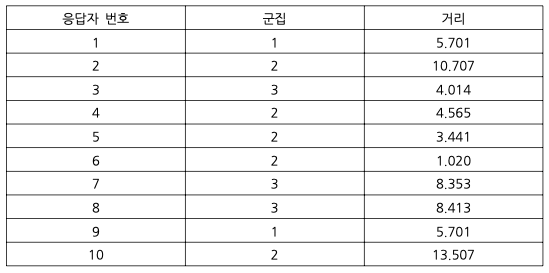
참고문헌 : Big Data 시대에 반드시 알아야 할 기초 통계지식/Ubion
'통계학 > 기초통계학' 카테고리의 다른 글
| 15차시 - 상관분석과 회귀분석 (0) | 2020.02.22 |
|---|---|
| 14차시 - 두 모집단 차이에 대한 추론 (0) | 2020.02.20 |
| 13차시 - 주요 모수에 대한 가설검정 (0) | 2020.02.19 |
| 12차시 - 표본크기 결정 및 가설검정 기초 (0) | 2020.02.18 |
| 11차시 - 표본비율 및 표본분산의 확률분포 (0) | 2020.02.17 |



