10차시 - 선형연립방정식과 해 (1)

1. 선형연립방정식

1) 선형연립방정식이란?

n개의 변수 x1, x2, ... , xn으로 이루어진 m원의 연립 1차 방정식

 

연립 1차 방정식을 행렬과 벡터를 이용하여 표현

 

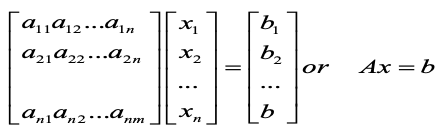
• 한 개 혹은 여러개인 경우

 

• 무한히 많은 경우(부정)

 

• 없는 경우(불능)

 

 

2) 선형의존이란?

• 하나의 방정식이 다른 방정식들의 합으로 표현 가능
• 만일 m번째 방정식이 다른 방정식들에 대해 선형 의존한다면, m번째 방정식은 다음 아래와 같이 표현

• 선형 의존인 방정식은 해를 찾는데 부가적인 정보를 줄 수 없음
  -> 선형 의존인 방정식을 제외하고 근을 구함

 

 

3) 선형의존의 예

• 3원 연립 방정식의 선형의존 예

 

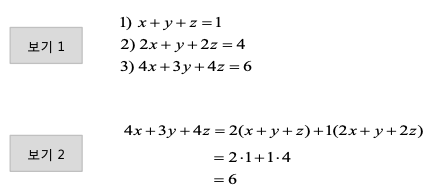
• 선형의존인 방정식은 전체 해에 영향을 주지 않음
  -> 선형 의존인 방정식을 제외하고 근을 구함

 

 

4) 불일치

• 한 방정식의 좌변은 다른 방정식의 좌변의 합으로 표현할 수 있음.
• 그 방정식의 우편은 다른 방정식의 우변의 합으로 표현할 수 없음.

 

 

5) 불일치의 예

• 3원 연립 방정식의 불일치 예

 

• 불일치라면 해당 연립방정식은 해를 가지지 않음
  -> 불능

 

 

 

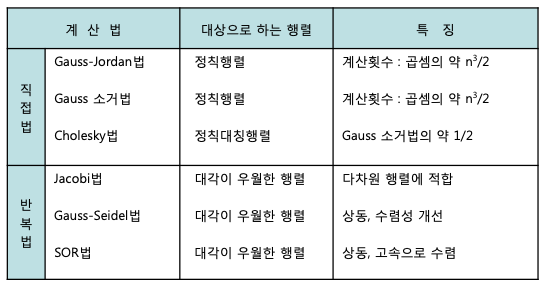
2. 연립방정식의 해법

1) 해를 구하는 방법

• 행렬 A가 정칙하면 역행렬이 있고 연립방정식 Ax=b의 해는 단 하나가 존재
  

• 이론적으로 해가 x=A^(-1)b이므로 역행렬 A^(-1)을 구한 후 이를 행렬의 백터 b를 곱하여 해를 구함.
• 행렬 A의 차수가 큰 경우, 역행렬을 구하는 것은 계산적으로 볼 때, 연립방정식의 해를 구하는 것보다 더욱 힘들고 매우 비효율적
• 따라서 직접법과 반복법을 이용하여 연립방정식의 해를 구함.

 

 

2) 선형연립방정식의 해를 구하는 다양한 방법